FP試験で出題される「6つの係数」って何でしょうね
同じFP試験の出題範囲でも、他の項目はどういう場面でそれが活用できるのか、あるいはどういう時に役立つのかがイメージできますが、この「6つの係数」というものだけは全くイメージが湧きません
計算式を覚えて、問題の解答を作るのはもちろん必要なことですが、それだけでは面白くないと思いませんか?
こういう問題を解けるようになって、そこから何を学べば良いのかということを考えてみました
6つの係数の定義とその使い方
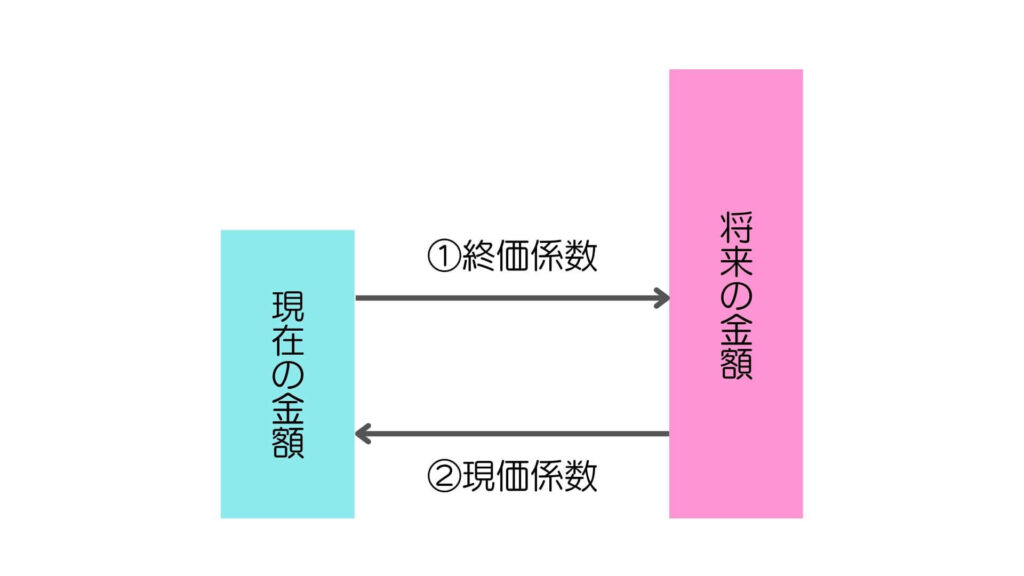
①終価係数
現在の額を一定の利率で運用した場合の将来の額を求める係数
⇒現在持っている1,000万円を、利回り2%で10年間運用するとしたら、いくら貯まることになるか
②現価係数
将来の必要金額を得るために、一定の利率で運用する場合の現在の必要金額を求める係数
⇒将来1,000万円を貯めるには、利回り2%で10年間運用するとしたら、現在いくら持っていなければならないか
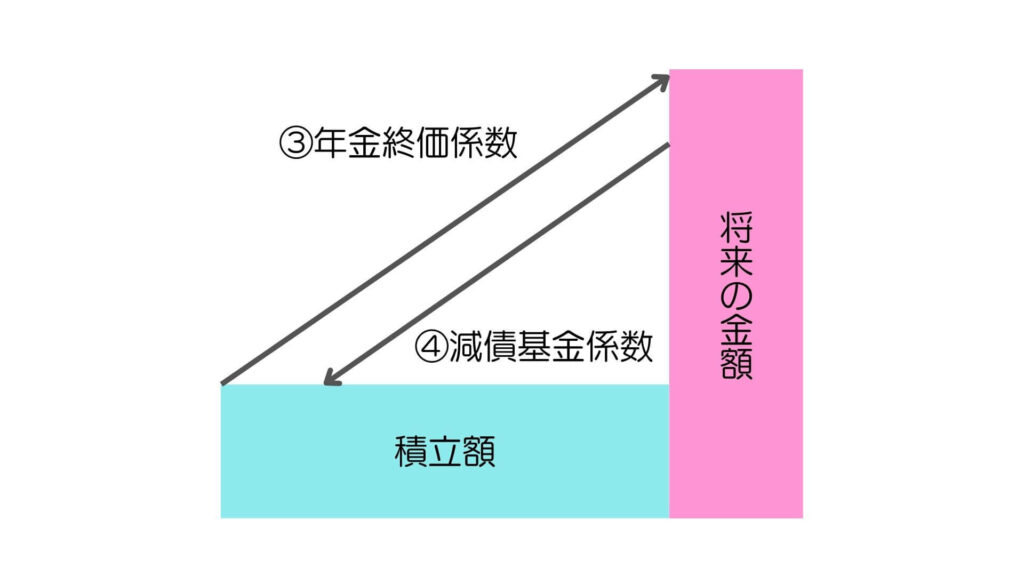
③年金終価係数
毎年の積立額から将来の積立合計額を求める係数
⇒毎年100万円を、利回り2%で10年間運用しながら積み立てると、いくら貯まることになるか
④減債基金係数
目標額を貯めるために必要な毎年の積立額を求める係数
⇒将来1,000万円を貯めるには、利回り2%で10年間運用しながら、毎年いくらずつ積み立てなければならないか
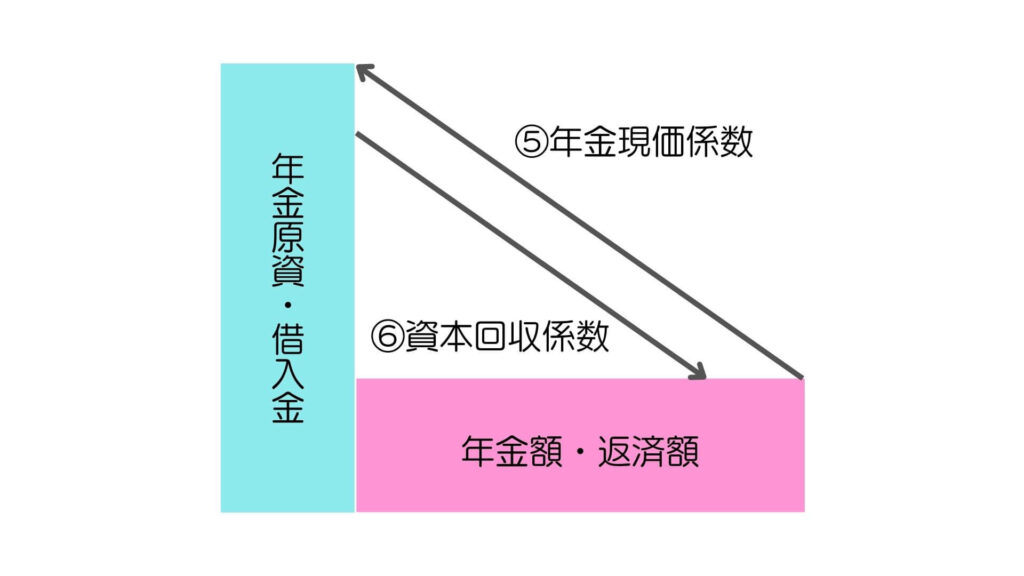
⑤年金現価係数
目標年金額を受け取るために現在必要な年金原資を求める係数
⇒ 10年間にわたって、毎年100万円ずつ引き出したいが、利回り2%で運用するとしたら、元本はいくら必要となるか
⑥資本回収係数
保有資産額を毎年の年金として受け取れる額を求める係数
⇒元本1,000万円を、10年間にわたって引き出したいが、利回り2%で運用するとしたら、毎年いくら引き出すことができるか
聞き慣れないワードの覚え方
6つの係数には普段聞き慣れないワードが含まれています
ここでは、そのワードごとの意味やイメージから、係数全体の意味を理解し覚えるという手法を説明していきたいと思います
✔ 終価:運用後の将来の(終わりの)価格
✔ 現価:運用前の元手の(現在の)価格
✔ 年金:毎年積み立てる or 取り崩す金額
≪覚え方≫
①終価係数
将来の価格を求める係数
②現価係数
元手の価格を求める係数
③年金終価係数
積み立て後の将来の価格を求める係数
⑤年金現価係数
取り崩しをするための元手の価格を求める係数
✔ 減債:債務を減らす(返済する)
✔ 基金:毎年積み立てる金額
≪覚え方≫
④減債基金係数
ここでは減債という言葉を一旦忘れた方が良いと思います
無理に理解しようとすると、むしろ頭が混乱します
その上で、ある目的のために毎年の積立額を求める係数と理解しましょう
✔ 資本回収:銀行がローンを回収するイメージ
≪覚え方≫
⑥資本回収係数
毎年の回収額を求める係数
6つの係数から学ぶべきこと
それでは、具体的な問題を解きながら、今回取り上げた6つの係数を理解し、何を学べばよいのかということを整理していきます
≪設問1≫
10年後に1,000万円を準備したいと考えている
期間中、年利2%で複利運用できるとすると、毎年いくら積み立てればよいか?
| (係数表) | 現価係数 | 減債基金係数 | 資本回収係数 |
| 10年 | 0.8203 | 0.09133 | 0.11133 |
(選択肢)
(1)82万円
(2)91万円
(3)111万円
この設問の解答は、(2)(1,000万円✕0.09133=91万円)となります
10年間で1,000万円を準備するのですから、運用することを考えなければ、毎年100万円(1,000万円÷10年)を積み立てればよいことになります
運用すれば、100万円以下で済むはずです
したがって、この設問では、(3)は絶対選んではいけません
この感覚が重要です
≪設問2≫
10年間、毎年100万円ずつ積み立てしようと考えている
期間中、年利2%で複利運用できるとすると、10年後にいくら準備できることになるか?
| (係数表) | 終価係数 | 年金終価係数 | 年金現価係数 |
| 10年 | 1.219 | 10.950 | 8.983 |
(選択肢)
(1)898万円
(2)1,095万円
(3)1,219万円
この設問の解答は、(2)(100万円✕10.950=1,095万円)となります
10年間、毎年100万円を積み立てるのですから、運用することを考えなければ、10年後に1,000万円(100万円✕10年)を準備できることになります
運用すれば、1,000万円以上になるはずです
したがって、この設問では、(1)は絶対選んではいけません
この感覚が重要です
時間の経過とともにお金の価値は変化していきます
将来になれば増えるし、過去に戻れば減ります
このようにお金を取り扱える感覚が重要なのです
自分の金融資産を投資で運用している人は、みんなその感覚でものごとを考えているはずです
今すぐに貰う100万円と10年後に貰う100万円は、どちらが良いか?
今すぐに払う100万円と10年後に払う100万円は、どちらが良いか?
どちらでも良いではなく、即座に選択できるお金の感覚の鋭さを磨いてほしいという期待が込められた設問であると思います



コメント